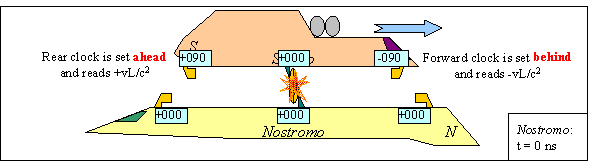
Let's look at two events in our Nostromo-Sulaco encounter..
The first is the destruction of the antennas, which happens at time zero according to both Sulaco's and Nostromo's antenna-clocks. We can define the origins of the two ships' coordinate systems to be at the antennas, though the coordinate system of one ship is seen to be moving when observed from the other ship.
The second event is the arrival of the light flash at Sulaco's forward periscope. According to Nostromo, this took place at t = 300 nsec and x = 300 feet, since Sulaco's forward periscope was moving away from the explosion. However, according to Sulaco, this event took place at time 150 nsec and position 150 feet since that is the time it took light to travel the 150 feet separating the antenna from the periscope in the Sulaco's rest frame.
The interval between the two events is just the difference
in the x,t coordinates of the events. We can use notation like this: 
and 
to
describe the intervals in the two frames of reference.
We'd like to figure out how to calculate the intervals in one frame of reference (say the Sulaco's) if we know the intervals as measured by observers in the other frame.
Since Sulaco's clocks run slowly (according to
Nostromo),
and the forward clock on Sulaco is out of synch with the antenna
clock (again, according to Nostromo), 
will
satisfy
.The first term to the right of the equal sign corresponds to the time-dilated amount of time that will pass on a Sulaco clock between the two events, while the second term takes into account the missynchronization between Sulaco's antenna and periscope clocks (as seen from Nostromo).
With a little algebra we find:
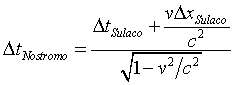.Notice that this formula lets us calculate the time interval according to Nostromo if we know both of Sulaco's measurements. Keep in mind that v is a positive number when Sulaco is moving in the +x direction (to our right) in the Nostromo frame.
Now let's work on the other interval.
Nostromo sees Sulaco moving to the right,
so Nostromo will see Sulaco's forward periscope travel a
distance 
while
the light from the explosion is in transit.
According to Nostromo, the light has to travel not only the (Lorentz-contracted)
distance between Sulaco's antenna and periscope, but also the distance
that the Sulaco periscope has moved since the instant the explosion
took place.
We have:
.We can do some more algebra to find the Lorentz transformations:
.
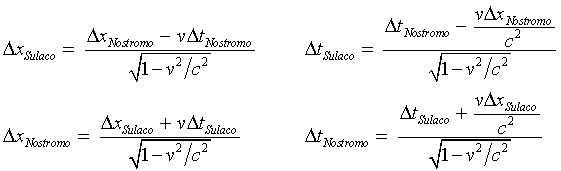When we know the spacetime interval between two events measured in one frame, we can predict the results of measurements made in another frame of reference using the Lorentz transformations.
