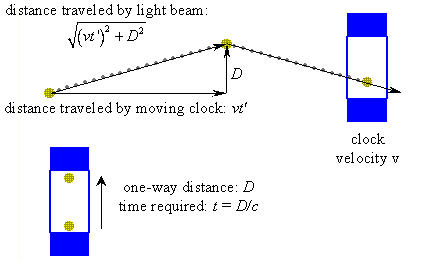
The idea is simple:
light always travels
about a foot
per nanosecond.
The light beam inside a moving light clock travels farther per "tick" than
the the light beam
inside the stationary clock. We can determine the time between ticks once
we know the distances involved.
The bottom-mirror-to-top-mirror trip only takes t = D/c in the stationary clock.
Let's say the corresponding trip takes t' in the moving clock. During time t', the clock moves to the right a distance vt'. The light beam travels along the hypotenuse of right triangle whose other sides have lengths vt' and D.
Since light always travels at c, we
must have 
.
We can solve for t' by squaring both sides and doing
some algebra. The result is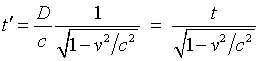 
.
Take a look
at what we've found: the moving clock
takes a factor of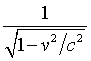 
longer to tick than does the stationary
clock, since its light beam travels farther per tick.
When 
the moving clock can take a very long
time
to tick compared to the stationary clock. Moving clocks (and
everything
else that's moving with respect to an observer) seem to be running
too slowly!
Fast-moving
people think slowly, respond slowly, get jokes
slowly,... relative to the observers who watch them.
